Dessa vez o artigo será mais técnico que meus últimos dois, onde expus uma análise mais sociológica do estado da Internet hoje, com o capitalismo de vigilância (a.k.a “capitalismo extremo”) e etc… De qualquer forma, tentarei escrever de uma forma que fique um pouco acessível a quem não é da área, mas que também seja interessante para quem já está um pouco familiarizado com programação e algoritmos!
Irei falar aqui sobre um tema que sempre me intriga quando tenho meus devaneios durante uma aula chata ou no chuveiro: a Teoria dos Seis Graus de Separação!
Introdução: O Jogo de Kevin Bacon
Em 1994, enquanto realizava uma entrevista, Kevin Bacon mencionou que já havia trabalhado, ou trabalhado com alguém que já havia trabalhado, com todas as pessoas de Hollywood. A partir disso, logo fizeram um jogo satírico em que os participantes, dado um ator de Hollywood, deveriam encontrar um outro ator que já esteve em um mesmo filme que o anterior, e assim por diante até chegar no Kevin Bacon. O objetivo seria conseguir achar o menor caminho entre o primeiro ator e o Kevin Bacon!
Apesar de ser uma brincadeira, o jogo levanta uma questão interessante: saindo da esfera de Hollywood e indo para toda a população, qual seria a maior distância social possível entre todas as pessoas do mundo?
A Teoria dos Seis Graus de Separação trata de encontrar uma resposta para essa questão :)
A Teoria dos Seis Graus de Separação
 https://en.wikipedia.org/wiki/File:Six_degrees_social_network.png (CC BY-SA 4.0)
https://en.wikipedia.org/wiki/File:Six_degrees_social_network.png (CC BY-SA 4.0)
A Teoria dos Seis Graus de Separação é, basicamente, a ideia de que todas as pessoas estão em, no máximo, 6 conexões distantes de cada uma. Podemos entender uma “conexão”, como sendo um laço de relação, ou até mesmo um aperto de mão, se quisermos simplificar (evita a discussão do que seria uma relação…). Na primeira vez que lemos isso, parece difícil de acreditar, certo? Principalmente porque a Teoria fala em todas as pessoas. Isso acontece porque tendemos a pensar de forma linear. Quer ver? Tente responder o seguinte problema:
Um recipiente possui uma população de bactérias. Sabendo que a população dobra a cada dia, e já se passaram 30 dias desde a primeira bactéria, em que dia o recipiente tinha metade da população atual?
Se você respondeu dia 15, você pensou de forma linear, o que é um equívoco. A resposta correta é dia 29. O problema diz que as bactérias dobram sua população a cada dia, ou seja, no dia zero temos 1, depois 2, 4, 8, 16, … 2^n, onde é o número de dias que se passaram. Ou seja, as bactérias cresciam exponencialmente, em um Progressão Geométrica, não de forma linear como seria em um Progressão Aritmética. Se no dia 30 temos X bactérias, tivemos X/2 bactérias no dia anterior, dia 29.
Veja como essa simples diferença no pensamento altera, e muito, resultado:

“Azul: exponencial | Verde: Linear | Eixo Y: População | Eixo X: Dias
Agora, de forma bem simplista e conservadora, vamos tentar estimar quantas pessoas, em média, uma pessoa conhece.
O Número de Dunbar
Se quisermos ter uma ideia da média de pessoas que uma pessoa conhece, não podemos deixar de considerar Número de Dunbar: proposto pelo antropólogo Robin Dunbar, 150 [pode variar] seria a medida do limite cognitivo teórico de pessoas com quais um indivíduo pode manter relações sociais estáveis, onde o indivíduo conhece cada membro do grupo e sabe em que relação cada indivíduo se encontra com os outros indivíduos do grupo.
Entretanto, este número inclui pessoas repetidas. Exemplo: se Alice conhece 150 pessoas, entre elas Bruno, e Bruno também conhece 150 pessoas, Alice estaria inclusa nessas 150. E ainda, como sou um Cientista da Computação [em formação], é claro que devo tentar analisar o pior cenário possível, e este cenário seria onde as pessoas são mais… antissociais! Por isso, sem nenhuma rigidez e classe, utilizarei o número 80 como sendo a média do número de pessoas diferentes que cada indivíduo conhece ou já conheceu em meu mundo fictício e, ainda, neste mundo as pessoas não possuem conexões de primeiro grau em comum!
Alice, que vive neste mundo, conhece 80 pessoas, dentre elas Bruno, que conhece 79 pessoas (tira a Alice), dentre elas Carlos, que conhece 78 pessoas (tira Bruno e Alice)…
Sabendo disso, queremos saber o número de conexões possíveis, partindo de Alice, até um pessoa qualquer que seja sua conexão de sexto grau. Bem, fazemos uma combinação, multiplicando a quantidade de pessoas que cada pessoa conhece. Dessa forma temos: c = 80x79x78x77x76x75 ~ 3 Bilhões.
Veja: sendo bem conservador e pessimista, com apenas 6 conexões, o número de conexões possíveis com pessoas diferentes já vai para cerca de 3 Bilhões! Lembrando que temos 7.9 Bilhões de pessoas no mundo. Agora dá pra entender de forma mais intuitiva que essa Teoria não parece tão absurda assim.
Vamos agora tentar modelar esse raciocínio de forma a ser mais fácil de desenvolver um algoritmo computacional para calcular o grau de distância entre duas pessoas. Teoria dos Grafos Uma Breve Revisão
Um grafo é uma estrutura de dados, na computação, em que os dados são representados por nós, ou vértices do grafo, que são ligados por outros nós através de arestas. Os grafos podem ser classificados de diversas maneiras, dentre elas:
- Grafo Direcionado: grafo cujas arestas possuem uma direção, tipo A -> B, mas não B -> A.
- Grafo Ponderado(valorado): possui arestas com pesos diferentes. Podem representar distância, um grau de dificuldade, etc…
Modelando Conexões Humanas com Grafos
Mesmo tendo uma noção bem simples de grafos, ainda é bem simples de pensar na aplicação de um grafo para modelar as conexões humanas. Sabemos que uma conexão é uma ligação entre duas pessoas. Se representarmos cada pessoa como um nó e cada relação como um vértice, pronto, temos um grafo!
Sabemos que o grafo não é direcional, pois não interessa para que direção eu estou indo, apenas a conexão em si e que, a priori, não é valorado (pode ser valorado se quisermos otimizar de alguma forma).
Computando o Grau de Conexão entre Duas Pessoas
Primeiramente, vamos relembrar que o grau de conexão entre duas pessoas é o número mínimo de conexões existentes entre elas. Traduzindo para a linguagem dos grafos: é o número mínimo de vértices que ligam dois nós, ou simplificando, a distância entre dois nós. E quando digo distância, quero deixar claro que é distância mínima que muitos autores citam, mas evito usar pois é redundante.
Bem, não há outro jeito de saber essa distância a posteriori se não percorrendo o grafo de alguma forma. E quando se trata de percorrer o grafo, existem diversas formas. Uma delas, a maneira burra, é usando o que chamamos de algoritmo de força bruta, testando todas as possibilidades. Mas fazer isso será tão ineficiente que, na prática, não irá resolver o problema.
Felizmente, há uma maneira um pouco mais inteligente e prática de fazer isso se pensarmos de forma gulosa!
Algoritmos Gulosos e Breadth-First Search (BFS)
Um algoritmo guloso é, particularmente interessante e tenho certeza que todos já utilizaram alguma vez na vida sem nem perceber. Geralmente é a primeira forma de algoritmo que pensamos quando queremos resolver um problema: buscamos achar uma solução ótima local e estudamos se resolver todos os problemas locais com esta solução resulta em uma solução ótima global.
Por exemplo: suponha que queremos saber o número mínimo de moedas necessárias para representar R$5,95. Minha abordagem, por algum motivo qualquer, poderia ser em tentar resolver o mesmo problema para R$4,00, para R$1,00 e para R$0,95. Ou seja, eu posso dividir meu problema em subproblemas, ou problemas locais. E quem sabe, se eu achasse a solução pra esses subproblemas eu poderia encontrar uma solução ótima global?
O algoritmo guloso entra aí: você acha soluções ótimas para problemas locais na esperança de encontrar uma solução ótima global. Digo “na esperança”, pois nem sempre isso será possível. No caso do problema das moedas acima, é possível sim encontrar uma solução ótima de forma gulosa! (se as moedas não tiverem ordenadas, usar programação dinâmica será muito mais eficiente)
Agora voltando ao problema de encontrar a distância entre duas pessoas, ou dois nós do grafo, é possível também resolver de forma ótima usando algoritmo guloso. A ideia é ir percorrendo o grafo de forma em que, dado um nó raiz, você percorra seus adjacentes primeiro e vai salvando a distância acumulada em cada nó percorrido. Para facilitar, podemos settar a distância inicial de cada nó para infinito (um número que seja maior que qualquer outro), e o da raiz para 0.
Esse simples algoritmo é conhecido como Breadth-First Search (Busca em Largura), ou BFS para os mais íntimos.
Bom, realmente é meio confuso, assim é melhor ver o GIF: Algoritmo Breadth-First Search
Note que os nós visitados ficam pretos, para que o programa não volte novamente neles. Uma forma prática e eficiente de fazer isso, que utilizei na minha implementação no Python, é utilizar um Set, pois seu custo de busca e inserção é constante.
Então assim fica a implementação:
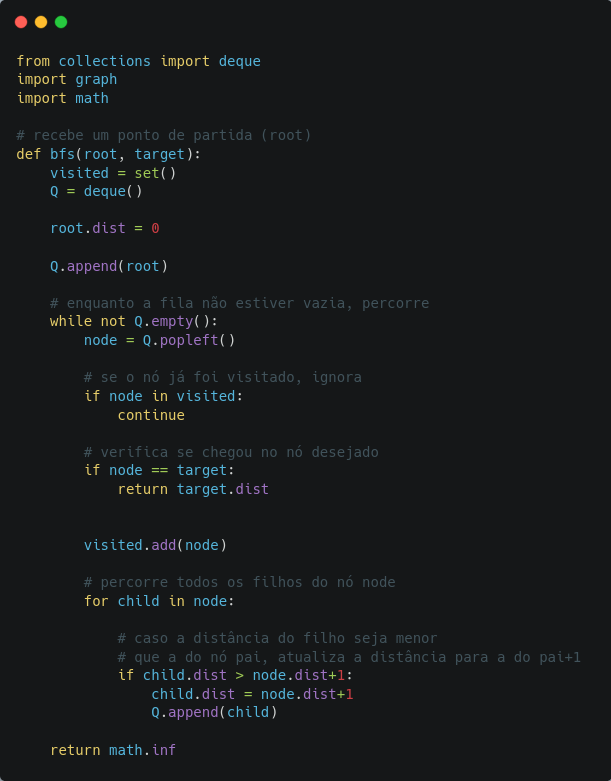
Agora, ao menos em teoria, podemos resolver esse problema apenas com esse simples algoritmo!
No próximo artigo pretendo colocar mais na prática essas ideias criando um programa para resolver o Six Degrees of Wikipedia.
Nota: O BFS é considerado um algoritmo guloso apenas caso seja utilizado para resolver um problema de otimização, como o do caminho mínimo.
Nota 2: considerei a biblioteca fictícia “graph” para não entrar no mérito da implementação do grafo aqui.
Nota 3: Utilizei bastante o termo “nó filho”, que serviria apenas para casos específicos de grafos, direcionados e acíclicos, conhecidos como árvores, mas como o grafo trabalhado seria acíclico e utilizamos apenas para o BFS, não faz diferença prática ele ter sido direcionado ou não. Bibliografia:
2- “Introduction to Algorithms” — Thomas H. Cormen, Et. Al — Capítulo 6 — “Algorítmos de Grafos”
3- “Algorithm Design” — Éva Tardos, Jon Klienberg — Capítulo 4, “Greedy Algorithms”